Le figure piane fanno parte del programma della scuola primaria. In realtà, entriamo a contatto con la geometria fin dai primi momenti della nostra vita. Il cerchio, il rettangolo, il triangolo, il quadrato e altri poligoni sono nello spazio che ci circonda.
Una figura geometrica piana è qualsiasi figura creata da linee che si trovano all’interno dello stesso piano e quindi ha solo due dimensioni: lunghezza e larghezza. Se la figura si trova su piani diversi è una figura geometrica solida che ha anche la profondità.
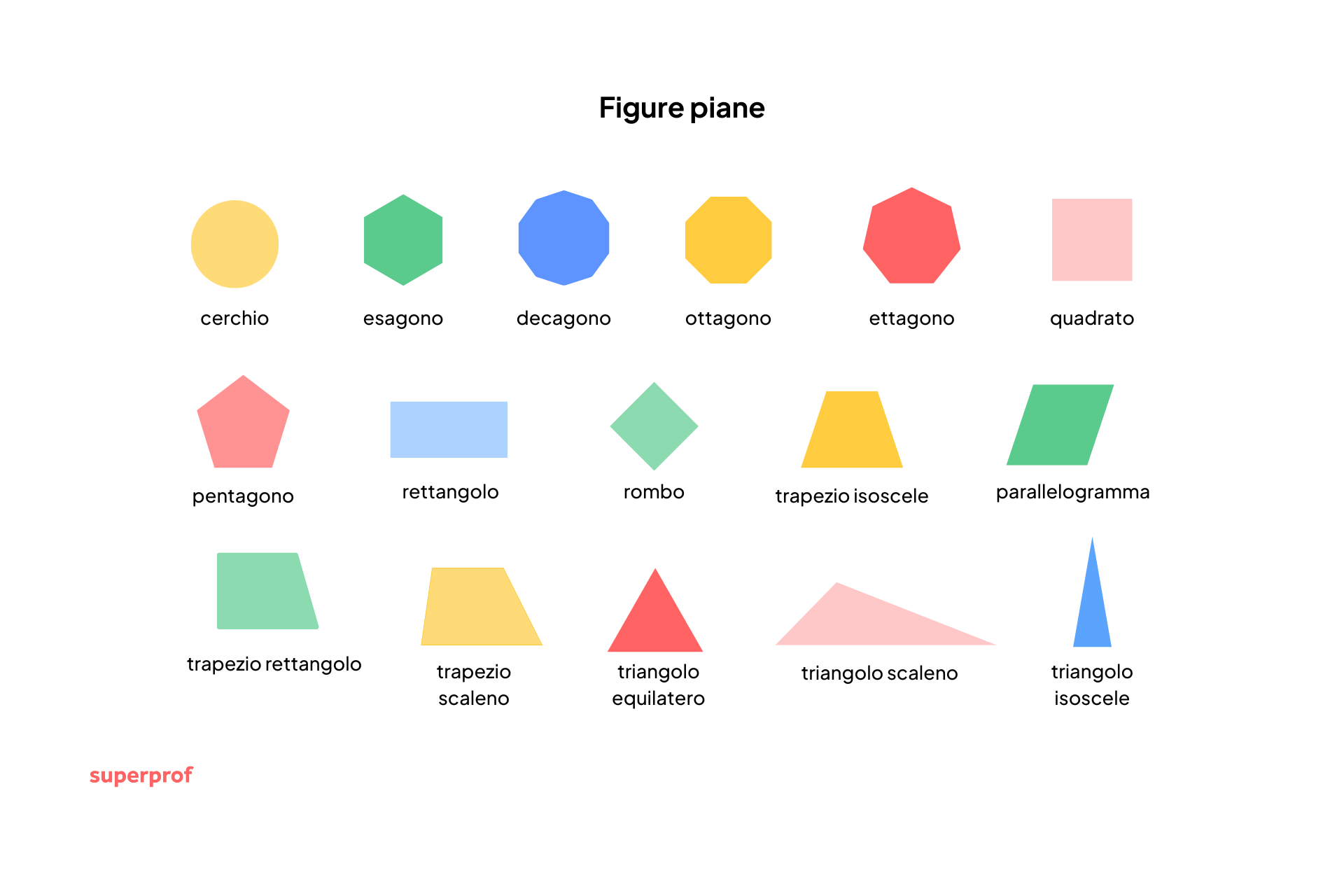
In questo articolo ti spiegheremo con semplicità cosa sono le figure piane e ti daremo anche qualche consiglio per imparare a riconoscere le figure geometriche con giochi divertenti, elencheremo i nomi tutti poligoni e molto altro. Ecco intanto alcune formule figure piane:
| Figura | Formula area (A) | Formula perimetro (P) |
|---|---|---|
| Triangolo equilatero | A = (b x h) : 2 | P = l x 3 |
| Triangolo isoscele | A = (b x h) : 2 | P = l1 + (l2 x 2) |
| Triangolo scaleno | A = (b x h) : 2 | P = l1 + l2 + l3 |
| Quadrato | A = l x l | P = l x 4 |
| Rettangolo | A = b x a | P = (l1 + l2) x 2 |
| Rombo | A = (D x d) : 2 | P = l x 4 |
| Trapezio | A= (b1+b2)×h:2 | P= a+b+c+d |
| Cerchio | A=π×r2 | 𝑃 = 2 × 𝜋 × 𝑟 |

La geometria e le figure piane
La geometria nasce per misurare i terreni dove si devono costruire case, palazzi, templi o altri tipi di edifici. La base della geometria sono delle figure tanto semplici quanto un punto.
Geometria deriva dal greco geōmetría, composto da gē̂ (“terra”) e -metría (“misurazione”). Il significato originario è quindi “misurazione della terra”. 1
Per comprendere la geometria delle figure piane, possiamo immaginare il mondo come un piano infinito, con soltanto due dimensioni: altezza e larghezza. È come un foglio di carta da disegno che non finisce mai, su cui possiamo tracciare punti: unendoli tra loro si creano linee, e quando queste linee si chiudono, nascono le forme geometriche.
Una linea retta è un insieme infinito di punti allineati, quindi è dritta e può essere orizzontale verticale e obliqua.
Quando due linee si incontrano, formano un angolo, con vertice nel punto d’incontro e lati che seguono la direzione delle linee. Chiudendo le linee si creano le figure geometriche: i poligoni, forme con almeno tre lati e tanti angoli quanti ne servono.
La matematica e, in particolare, la geometria, sono fondamentali per comprendere e modellare il nostro mondo. Il 27 novembre 2025, oltre 1.300 scuole italiane hanno partecipato alla prima competizione dell’anno del programma delle Olimpiadi Italiane della Matematica3, un evento che non solo celebra il talento degli studenti, ma promuove anche l’importanza della geometria come linguaggio universale.
La geometria ci insegna a leggere, comprendere e creare il mondo intorno a noi, dai disegni più semplici alle costruzioni più complesse. Ogni punto, linea e angolo ha un ruolo nel costruire l’armonia delle forme che vediamo ogni giorno.
Come riconoscere le figure geometriche piane
Per imparare a riconoscere le figure piane dobbiamo prima imparare a capire cos’è un poligono e poi classificare i poligoni in base al numero di lati, angoli e vertici che lo compongono.
Definizione di poligono
Il poligono2 è una figura geometrica piana formata da una linea spezzata chiusa. Se una forma geometrica chiusa ha una linea curva o mista, non si può definire un poligono. In sostanza ecco i poligoni quali sono:
Cosa è un poligono 📌
Una figura geometrica piana formata da una linea spezzata chiusa, composta esclusivamente da segmenti.
Cosa non è un poligono ❌
Una figura chiusa che presenta linee curve o linee miste (in parte curve e in parte spezzate).
Ricorda: il poligono ha solo linee spezzate e chiuse. Le linee curve o miste chiuse non formano i poligoni!
Gli elementi che compongono un poligono sono:
- Vertici: i punti in cui si incontrano due lati
- Lati: segmenti che collegano due vertici
- Angoli: lo spazio compreso tra due lati consecutivi
- Diagonali: segmenti che uniscono due vertici non consecutivi, che si trovano uno opposto all'altro
- Altezze: segmenti perpendicolari che collegano un vertice al lato opposto
- Perimetro: la lunghezza del contorno del poligono, quanto misura la linea spezzata che forma il poligono, quindi il contorno della figura geometrica piana. Preparati a imparare a memoria le formule figure piane!
- Superficie: la parte di piano racchiusa all’interno del poligono
Per riconoscere i vari poligoni basta osservarli attentamente e contare quanti vertici, angoli e lati hanno.
Un poligono con tre vertici, angoli e lati è un triangolo, se ha quattro vertici, angoli e lati è un quadrilatero, se ne ha cinque è un pentagono, se ne ha sei è un esagono. Un ettagono ha sette vertici, angoli e lati mentre un ottagono ne ha otto.
Come si chiama un poligono con 9 lati? 🧐
💡 Trucchetto utile: in un polgono il numero di lati, angoli e vertici è sempre lo stesso. 💡
Quindi, se vedi un poligono con cinque lati, avrà sicuramente anche cinque angoli e cinque vertici.
Ecco quindi i nomi tutti i poligoni:
- Triangolo (3 lati)
- Quadrato (4 lati)
- Rettangolo (4 lati)
- Rombo (4 lati)
- Parallelogramma (4 lati)
- Trapezio (4 lati)
- Deltoide (4 lati)
- Pentagono (5 lati)
- Esagono (6 lati)
- Eptagono (7 lati)
- Ottagono (8 lati)
- Ennagono (9 lati)
- Decagono (10 lati)
- Dodecagono (12 lati)
- Poligono con n lati (n lati)
Se frequenterai delle ripetizioni matematica roma nord o in qualsiasi altra città, scoprirai che i poligoni possono essere regolari e non regolari.
Poligoni regolari:
- Tutti i lati uguali
- Tutti gli angoli uguali
- Sempre convessi
Poligoni irregolari:
- Possono avere solo i lati uguali oppure solo gli angoli uguali
- Possono essere concavi
I poligoni sono concavi se sono attraversati dal prolungamento di almeno due lati. (In maniera poco scientifica, è come se un angolo guardasse all’interno, invece che all’esterno.)

Per riassumere i poligoni sono:
Equilaterali
se hanno tutti i lati uguali
Equiangoli
se hanno tutti gli angoli uguali
Regolari
se hanno tutti i lati e gli angoli uguali
Ora che sappiamo cos’è una figura geometrica piana e come si classificano i poligoni, vediamo in dettaglio quali sono le caratteristiche delle maggiori figure geometriche piane.
Figure geometriche piane: i triangoli
Il triangolo in geometria è una figura piana: un poligono con tre vertici, tre angoli e tre lati. Visto che il numero tre piace molto ai triangoli, si possono classificare in tre tipi:
Triangolo scaleno - ha tutti i lati di dimensioni diverse
Triangolo isoscele - ha due lati congruenti, ossia uguali.
Triangolo equilatero - ha tutti e tre i lati uguali (è un poligono regolare)
Come si calcola il perimetro del triangolo? Il perimetro è dato dalla somma dei lati: l1+l2+l3.
In un triangolo equilatero i tre lati sono uguali quindi il perimetro si ottiene moltiplicando il lato per tre. P=lx3

Figure geometriche piane: i quadrilateri
I quadrilateri sono poligoni che hanno:
- quattro lati
- quattro angoli
- quattro vertici
- due diagonali

Ricorda che le diagonali sono segmenti che uniscono i vertici opposti. Cerchi lezioni private matematica palermo? Consulta il portale di Superprof! Esistono diversi tipi di quadrilateri, che si distinguono in base alla lunghezza dei lati, all’ampiezza degli angoli e alle proprietà delle diagonali.
Quadrato
Un'altra figura piana è il quadrato, un parallelogramma che ha:
- quattro lati uguali
- quattro angoli retti
- due diagonali uguali, che si incontrano al centro e dividono la figura in quattro parti simmetriche
Il perimetro del quadrato è P = l x 4.
Ricorda che il quadrato ha tutti i lati uguali quindi per trovare il perimetro, ossia la lunghezza del contorno di questa figura geometrica piana, dovremmo fare lato+lato+lato+lato, quindi dovremmo ripetere il lato quattro volte. Ecco perché lato per quattro.
L’area del quadrato è lato per lato: A = l x l
📏 Perimetro del quadrato
Il perimetro è la misura del contorno della figura:
Rettangolo
Il rettangolo è un parallelogramma che ha:
- lati opposti uguali
- quattro angoli retti
Il perimetro di questa figura piana è la somma dei lati che sono uguali a due a due, quindi è P = (l1 + l2) x 2.
Tra le formule figure piane sicuramente c'è da imparare questa: l’area del trinagolo è base per altezza: A = b x a
Rombo
Il rombo è un parallelogramma che ha:
- quattro lati congruenti e gli angoli opposti uguali
Le due diagonali sono diverse e sono diagonale maggiore e diagonale minore.
Il perimetro, come per il quadrato è pari a P = l x 4
Ecco un'altra delle formule figure piane: l’area del rombo si calcola trasformandolo in un rettangolo e facendo diagonale maggiore, D, per diagonale minore, d, diviso due.
A = (D x d) : 2
Trapezio
I trapezi sono dei quadrilateri che hanno una coppia di lati paralleli (almeno due lati sono paralleli).
Ricorda che le rette parallele hanno sempre la stessa distanza tra loro e non si incontrano mai.
Uno dei due lati paralleli è più lungo e viene chiamato base maggiore; il lato parallelo più corto viene chiamato base minore.
I parallelogrammi hanno due coppie di lati paralleli. In altre parole, i lati sono paralleli a due a due.
Domanda: i parallelogrammi sono anche dei trapezi?
Sì, perché per definizione i trapezi hanno una coppia di lati paralleli, cosa che hanno anche i parallelogrammi che in più hanno anche la seconda coppia di lati paralleli.
Figure geometriche piane: i poligoni regolari
Lo potrai scoprire al tuo prossimo corso di matematica online: i poligoni regolari hanno tutti i lati e tutti gli angoli uguali. Il triangolo equilatero e il quadrato sono due esempi di poligoni regolari che abbiamo già visto. I lati e gli angoli del poligono possono essere molti di più e quindi abbiamo:
- Pentagono
- Esagono
- Ettagono
- Ottagono
- Ennagono
- Decagono
- Endecagono
È facile calcolare l’area di un poligono regolare: basta moltiplicare il lato per il numero dei lati. P = l x n.
Da qui puoi ricavare la formula inversa per cui il lato = P : n e naturalmente n= P : l.
Domanda: come si calcola il perimetro di un dodecagono regolare? Riuscirai a imparare tutte le formule figure piane? Ponitelo come la tua prossima sfida!
Giochi con le figure piane
E sappiamo che per imparare la teoria a volte la pratica può venire in aiuto e risultare mooolto efficace: in questo modo ci si diverte e intanto si impara! Riconoscere le figure geometriche infatti può diventare un gioco divertente e creativo! Attraverso attività pratiche, sfide con amici o compagni di classe, è possibile memorizzare forme, proprietà e caratteristiche delle figure in modo semplice e naturale. Dai giochi di osservazione alla creazione di poligoni, fino alla tombola delle figure geometriche, ogni attività aiuta a collegare la matematica alla realtà quotidiana e a stimolare la curiosità.

Caccia alle figure in classe
Per imparare a riconoscere le figure piane sfida i tuoi amici a trovare degli oggetti in classe a forma di… quadrato, triangolo, rettangolo... o addirittura un cerchio!
Osservate attentamente l’ambiente e cercate di individuare il maggior numero possibile di figure. Questo gioco aiuta a collegare la teoria alla realtà quotidiana.
Creazione di poligoni su cartoncino
Usa il righello per disegnare dei poligoni su un cartoncino colorato. Fanne tanti, di diverse forme e dimensioni. Scambia i poligoni con i compagni e divertitevi a fare un collage con le forme geometriche piane che avete creato. Potete appenderlo in classe e prendere spunto dai quadri di alcuni artisti come Kandinskij, che amava usare forme geometriche e colori vivaci nelle sue opere.
Tombola
Per un gioco più strutturato, potete creare una tombola delle figure geometriche piane.
- Costruite una tabella con tutte le figure che avete studiato.
- Uno dei compagni o l’insegnante estrae a sorte una figura.
- Chi possiede quella figura sulla propria tabella deve dire le proprietà della figura per poter fare punto.
Questo gioco stimola la memoria, la velocità di osservazione e la capacità di descrivere le caratteristiche delle figure geometriche.
Applicazioni pratiche delle figure piane
Sicuramente a fine di questo articolo avrai imparato i poligoni cosa sono. Come dicevamo all'inizio dell'articolo, le geometriche piane non sono solo concetti astratti da studiare a scuola che poi finiranno nel dimenticatoio: in realtà potremmo incontrarle ogni giorno in architettura, arte, design e ingegneria. Comprendere le loro proprietà ci aiuta a interpretare meglio il mondo che ci circonda e a sviluppare competenze pratiche.

Figure piane in architettura e design
Architetti e designer utilizzano forme geometriche piane per progettare edifici, interni e mobili. Ad esempio, rettangoli e quadrati definiscono la struttura delle stanze, mentre triangoli e trapezi garantiscono stabilità a ponti e tetti. Nel design d’interni, le figure geometriche aiutano a creare equilibrio, armonia e movimento visivo, guidando lo sguardo e valorizzando gli spazi. Ecco qui un esempio pratico di quanto l'architettura si basi sulla geometria! Forse è banale affermarlo, ma vederla applicata fa comunque un certo effetto!
Figure piane nell'arte e nella pittura
Molti artisti sfruttano o hanno sfruttato le figure geometriche piane per comporre opere armoniose e dinamiche. Pensiamo a pittori come Mondrian e Kandinskij, ma anche a Picasso: le linee e i poligoni sono alla base del loro stile. I cerchi, i triangoli e i rettangoli sono spesso presenti in loghi, manifesti e illustrazioni. Comprendere le forme aiuta anche a analizzare la prospettiva e la composizione dei quadri. Insomma, si pensa che l'arte sia creatività, astrazione, istinto e ispirazione, e invece a volte si fonda sui principi della geometria e suelle sue forme.
Figure piane nella tecnologia e ingegneria
In ingegneria, elettronica e meccanica, le figure piane sono fondamentali per progettare componenti, circuiti e strutture complesse.
- Triangoli e trapezi: utilizzati per costruire strutture solide e stabili, come ponti, gru e tetti, grazie alla loro capacità di distribuire le forze in modo uniforme.
- Rettangoli e quadrati: servono per ottimizzare spazi e materiali, ad esempio nei circuiti elettronici, nei pannelli solari o nella progettazione di macchine industriali.
- Cerchi e poligoni regolari: spesso presenti nei meccanismi rotanti, ingranaggi e ruote, permettono movimento fluido e precisione nei macchinari.
Anche nel design dei veicoli e delle macchine, le figure piane aiutano a definire forme funzionali ed estetiche, combinando efficienza e bellezza.
Fonti
- “Geometrìa.”Vocabolario Treccani, Treccani, n.d., https://www.treccani.it/vocabolario/geometria/.
- “I poligoni: come sono e come si classificano.” Sapere Virgilio, 27 Maggio 2024, https://sapere.virgilio.it/scuola/elementari/geometria/poligoni/poligoni-classificazione
- Lab, & Lab. "Giochi di Archimede 2025." Progetto Olimpiadi della Matematica, 11 dic. 2025, https://olimpiadi.dm.unibo.it/2025/12/11/giochi-di-archimede-2025/.
Résumer avec l'IA :
















