L'insieme di Julia è una meraviglia della matematica, offre forme infinitamente complesse che emergono da una semplice equazione. Come il suo celebre cugino, l'insieme di Mandelbrot, racconta il fascino dei frattali, in cui ogni ingrandimento rivela nuovi modelli auto-simili.
Esplorando le proprietà di questo insieme, si scopre una ricchezza di dettagli matematici che collega la teoria dei sistemi dinamici ad applicazioni concrete, ispirando al contempo l’arte e la scienza.
Nell’analisi complessa, l’insieme di Julia di una funzione è formato da quei punti in cui, se applichi la funzione più e più volte, il risultato si comporta in modo imprevedibile. Anche un piccolo cambiamento iniziale può portare a un risultato completamente diverso, come se il sistema cambiasse per un dettaglio minuscolo.
Se vuoi conoscere meglio il mondo dei frattali continua a leggere l'articolo!

La scoperta dell'infinito grazie a Gaston Julia

La sola cosa che sappiamo per certa riguardo all’infinito è che le discussioni su di esso sono infinite.
Joop Goudsblom
E tu ti sei mai chiesto se l'infinito esiste?
È proprio ciò che si sono chiesti, nel corso della loro carriera e durante le ore di ripetizioni matematica, diversi ricercatori e scienziati, come Gaston Julia. Matematico francese nato nel 1893 in Algeria, fu segnato profondamente dal suo impegno nella Prima guerra mondiale, durante la quale riportò gravi ferite al volto. Gaston Julia intraprese comunque una brillante carriera accademica come professore di matematica:
- Dopo un dottorato in matematica applicata, avviò ricerche sulle dinamiche olomorfe, che studiano la complementarità degli insiemi in base al loro comportamento.
- Dopo il dottorato, insegnò all’École Normale Supérieure, dove formò intere generazioni di matematici.
Prima dei suoi studi, le basi teoriche degli insiemi frattali e dei sistemi dinamici si stavano già delineando nel XIX secolo. Matematici come Pierre Fatou, Henri Poincaré e Félix Klein avevano esplorato i comportamenti complessi delle funzioni olomorfe e delle trasformazioni iterative.
Già a partire dagli anni 1910, il lavoro di Julia si inserisce nella ricerca sulle funzioni iterative e sullo studio dei comportamenti complessi, in un contesto difficile per l’Europa dell’epoca.
La dinamica olomorfa è una nuova classe matematica nata dai lavori di Gaston Julia e Pierre Fatou sulle funzioni razionali complesse. Essa studia il comportamento delle successioni iterative nel piano complesso, rivelando strutture frattali. Questa disciplina ha aperto nuove prospettive nell’analisi complessa e nello studio dei sistemi dinamici.
Sebbene Julia avesse pubblicato i suoi risultati già nel 1918, le sue scoperte rimasero relativamente nell’ombra fino alla loro riscoperta negli anni ’70, grazie ai progressi informatici e, in particolare, al ruolo di Benoît Mandelbrot, che teorizzò il celebre insieme di Mandelbrot basandosi proprio sulle teorie di Julia.
Va detto anche che Julia è una figura controversa nella storia della scienza, a causa delle accuse di collaborazione con il regime durante la Seconda Guerra Mondiale, motivo per cui molti accademici francesi lo esclusero successivamente dai principali circoli scientifici.
In ogni caso, l’insieme di Julia resta un pilastro delle moderne matematiche applicate. Scopriamo ora nel dettaglio l’insieme di Julia e l’equazione che lo genera!
Gaston Julia ha mostrato come il comportamento infinito e caotico può essere contenuto in equazioni finite, e che i suoi effetti sono visibili in modo illimitato attraverso le iterazioni e le strutture frattali. Il suo lavoro ha ampliato la nostra comprensione delle strutture matematiche infinite, creando un legame tra matematica, arte e scienza computazionale, e rivelando l'infinito non come un concetto astratto, ma come qualcosa che può essere esplorato, visibile e realizzabile.
Studio dell'insieme di Julia: un'equazione con infinite forme
Se oggetti come il fiocco di Koch possono essere studiati nell’ambito della matematica applicata, l’insieme di Julia si concentra su insiemi più ampi.
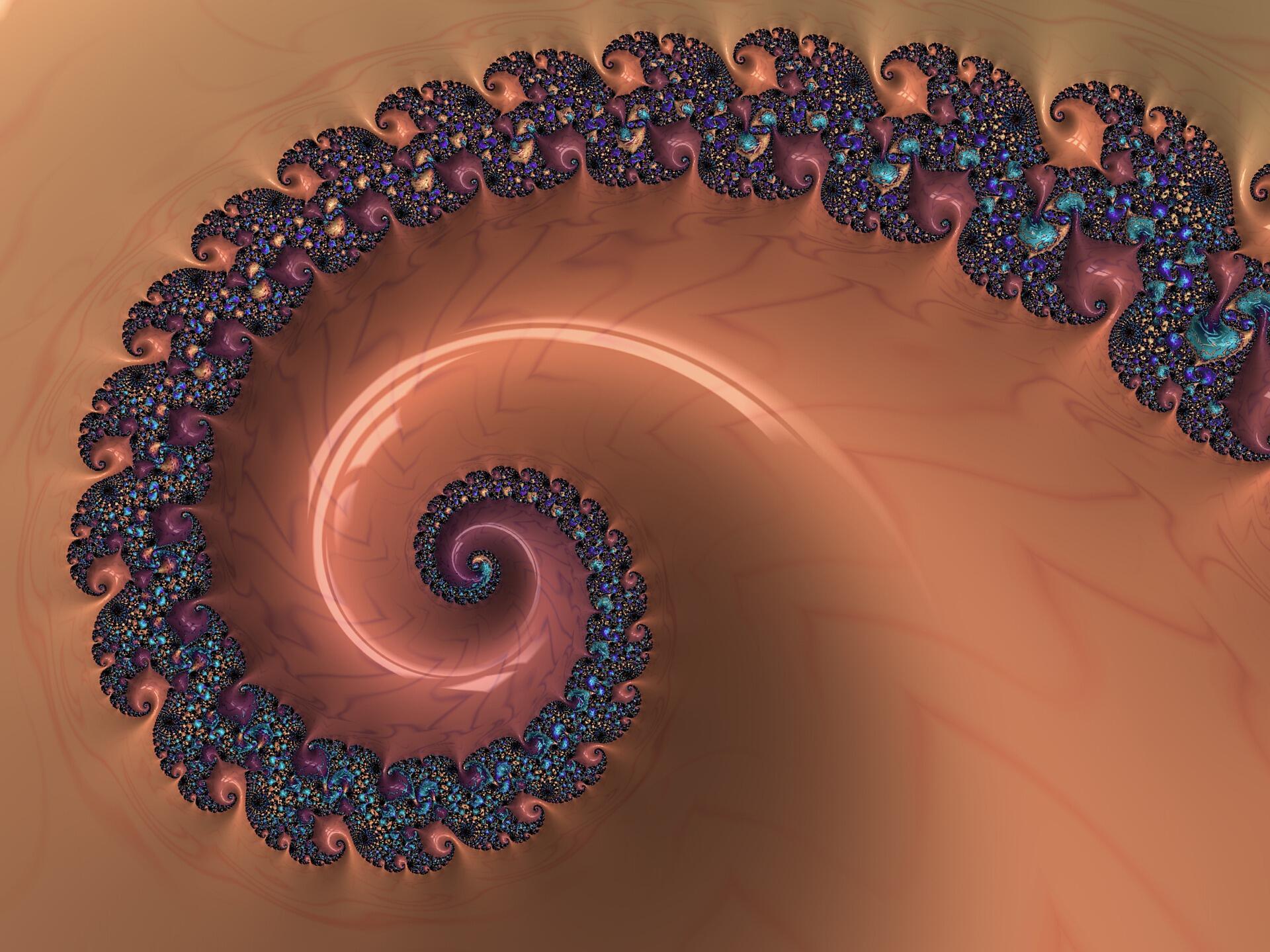
Questi ultimi - chiedi spigazioni ulteriori al tuo insegnante di ripetizioni matematica torino - rispondono a una funzione iterativa z = z2 + c e al suo legame con la dinamica complessa, dando origine a oggetti matematici infinitamente dettagliati.
L’insieme è definito dai punti che restano in una zona limitata sotto l’iterazione della funzione:
- A seconda dei valori di c, l’insieme di Julia può essere complesso e connesso (una forma continua), oppure frattale e disconnesso (polvere di punti).
- In base ai valori di c, l’insieme di Julia mostra forme infinitamente varie, che vanno da strutture semplici a motivi estremamente dettagliati e visivamente ipnotici.
Si individuano 4 principi fondamentali dell'insieme di Julia:
- Forma matematica: l'equazione di Julia si basa sull'iterazione di una funzione quadratica complessa, i cui fattori sono numeri complessi.
- Divergenza o stabilità: applicando ripetutamente questa funzione a un punto, si osserva se tende verso l'infinito (divergenza) oppure resta entro una zona limitata (stabilità).
- Definizione dell’insieme: l'insieme di Julia è formato dai punti le cui iterazioni non divergono. La sua forma dipende dal parametro complesso c.
- Collegamento con Mandelbrot: l'insieme di Mandelbrot classifica i valori di c in base alla stabilità del corrispondente insieme di Julia, mettendo così in relazione le due strutture frattali.
Mentre l’insieme di Mandelbrot esplora i comportamenti di questa equazione in funzione dei parametri complessi, l’insieme di Julia si concentra sui risultati ottenuti per valori fissi di tali parametri. In altre parole, ogni punto dell’insieme di Mandelbrot corrisponde a un insieme di Julia unico, e i due insiemi condividono motivi frattali simili, pur presentando strutture visive differenti.
Immagini ipnotiche e complesse di frattali di Julia
Gli insiemi di Julia generano immagini affascinanti, spesso paragonate a opere d’arte naturali per via delle loro strutture organiche e infinite, simili a quelle che si osservano nei frattali vegetali o geologici. Un esempio concreto di frattale è il corallo marino, che unisce irregolarità e precisione.

L'insieme continua con la seguente equazione:
fc(z)= z2 + c
Queste forme rientrano in due grandi categorie:
- Gli insiemi connessi
- Gli insiemi totalmente disgiunti
Dunque:
- Se c appartiene all’insieme di Mandelbrot, allora l’insieme di Julia corrispondente è connesso, formando una struttura continua. Questi insiemi mostrano forme filamentose e ricche di dettagli, che ricordano strutture organiche come i coralli o le nervature delle foglie. Ad esempio, per c = 0, l’insieme di Julia è un semplice disco, mentre per valori complessi assume forme più complesse e tortuose.
- Se c non appartiene all’insieme di Mandelbrot, allora l’insieme di Julia è totalmente disgiunto, composto da una nuvola di punti separati, formando quella che viene chiamata una "polvere di Fatou". Questi insiemi presentano strutture sparse in cui ogni punto è isolato dagli altri.
Non è abbastanza chiaro? Parlarne con il tuo prof di ripetizione matematica milano!
Gli insiemi di Julia sono estremamente sensibili alle variazioni di c. Una minima modifica del parametro comporta trasformazioni spettacolari, dando origine a spirali, strutture ramificate o motivi con ramificazioni infinite.
Grazie ai calcoli informatici, è possibile visualizzare queste strutture con un livello di dettaglio vertiginoso, rivelando motivi autosimili a ogni livello di ingrandimento.
Geometria complessa: dalla teoria alle applicazioni concrete dell'insieme di Julia

Soprattutto grazie ai lavori di Julia da parte di Mandelbrot e di altri ricercatori, i frattali hanno potuto contribuire all’approfondimento delle conoscenze sulla dinamica complessa.
Lo studio degli insiemi di Julia, ha ampliato la comprensione dei sistemi non lineari e del loro comportamento caotico, in particolare in ambiti come l’informatica, la modellizzazione scientifica e le arti, rafforzandone l’importanza in numerosi settori.
Ecco una panoramica degli utilizzi dell’insieme di Julia nell’arte digitale, nella modellizzazione e nella scienza.
Oltre ad altri oggetti frattali come il triangolo di Sierpinski, che non ha più segreti dopo essere stato ampiamente diffuso nelle aule di tecnologia, l’insieme di Julia ha ispirato molte altre realizzazioni.
Se fossi un punto nell'insieme di Julia, quale forma avresti? 🧚♀️
Le immagini frattali svolgono un ruolo fondamentale in diversi ambiti artistici e tecnologici:
- Nell’arte digitale, vengono utilizzate per creare opere visive ipnotiche e complesse, dove i motivi si ripetono all’infinito con una ricchezza di dettagli affascinante. Gli artisti sfruttano le proprietà di autosimilarità per generare figure uniche e dinamiche.
- Nel graphic design, i frattali servono a progettare motivi di sfondo, texture organiche ed elementi visivi coinvolgenti, soprattutto nel web design, la moda o l’illustrazione. La loro capacità di imitare forme naturali come nuvole o rami conferisce loro un fascino particolare.
- Nel cinema e nell’animazione, queste strutture matematiche sono ampiamente usate. Film di fantascienza e fantasy integrano i frattali nella progettazione di paesaggi extraterrestri o effetti speciali. Software come Houdini o Mandelbulb3D permettono di generare ambientazioni ultra-dettagliate partendo da equazioni frattali, offrendo un’estetica al tempo stesso realistica e surreale.
cioè una cifra incommensurabile
Più recentemente, i computer hanno assunto un ruolo fondamentale nella visualizzazione degli insiemi di Julia, permettendo di esplorarne la complessità con una precisione senza precedenti. Grazie ai progressi tecnologici, i ricercatori possono generare immagini ad alta risoluzione, rivelando dettagli infinitamente piccoli che sarebbe impossibile disegnare a mano.
Gli algoritmi moderni consentono di effettuare zoom profondi all’interno di queste strutture, svelando motivi auto-simili che si ripetono su diverse scale. Con software come Ultra Fractal o Mandelbrot Explorer, è possibile navigare in questi paesaggi matematici e scoprirne la ricchezza nascosta.
Infine, l’intelligenza artificiale e il calcolo ad alte prestazioni hanno ulteriormente migliorato la generazione di queste immagini. I frattali non sono più solo curiosità matematiche, ma sono diventati strumenti di studio e ispirazione per la scienza, l’arte e la tecnologia. Questo significa che l’informatica ha reso accessibili al grande pubblico questi oggetti astratti e affascinanti.
Ora che conosci tutto sull’insieme di Julia, puoi esercitarti a visualizzare i frattali usando i software disponibili!
Riassumi con IA















