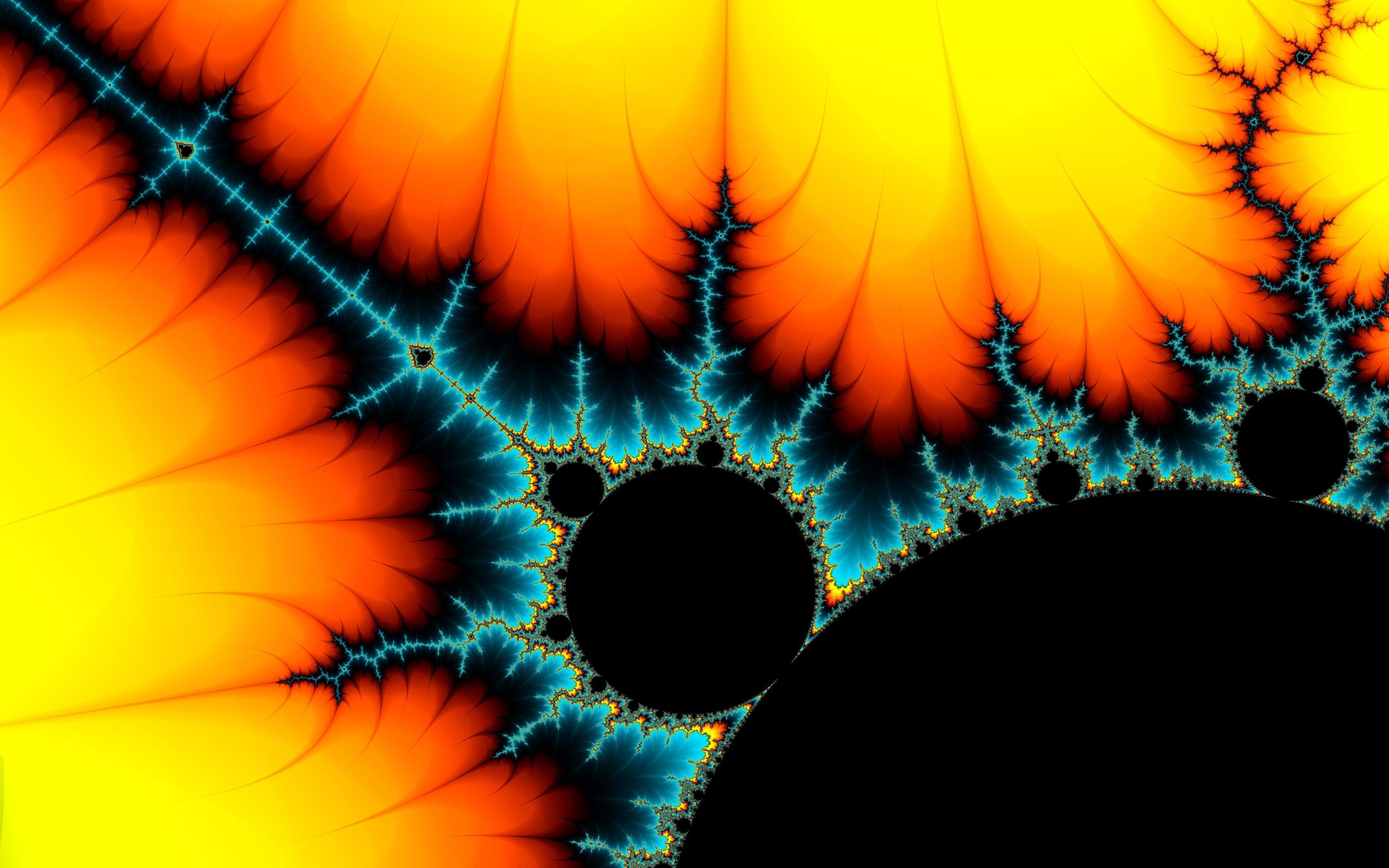
L'insieme di Mandelbrot è una delle figure più iconiche della matematica moderna e illustra la bellezza e la complessità dei frattali. Scoperto da Benoît Mandelbrot negli anni '80, si basa su un'equazione semplice ma che genera forme infinitamente dettagliate, in cui ogni ingrandimento rivela nuove affascinanti strutture.
Le ricerche di Mandelbrot rivoluzionarono la comprensione delle dinamiche complesse e non solo furono significative nella matematica, trovarono applicazione anche nella scienza, nell'arte e nella tecnologia.
Mandelbrot è un esempio perfetto di come questi due mondi si possano incontrare e di come pensare fuori dagli schemi possa portare a scoperte rivoluzionarie.
Per approfondire il mondo dei frattali o degli oggetti frattali, come definiti da Mandelbrot, continua a leggere il nostro articolo. Parleremo di:
- chi era Mandelbrot
- cos'è l'insieme di Mandelbrot
- le applicazioni dei frattali di Mandelbrot
- l'eredità di Mandelbrot

Mandelbrot, visionario delle forme infinite
In poche parole, Mandelbrot collegando geometria, caos e strutture naturali, dimostrò che i frattali offrono un nuovo linguaggio per comprendere il mondo.

Nato nel 1924 in Polonia e naturalizzato francese, Mandelbrot esplorò ambiti diversi, dalla matematica pura all’economia e alla fisica. Scienziato visionario a tutti gli effetti, è anche la figura che ha dato origine ai frattali moderni.
Dopo un'infanzia complicata, Mandelbrot partì per gli Stati Uniti per studirare matematica e scienze. Inizialmente deluso dal Caltech di Pasadena e dai suoi professori che non erano molto interessati al suo stimolo intellettuale, scelse infine di scrivere la sua tesi a Parigi nel 1952, sul tema "Contributo alla teoria matematica dei giochi di comunicazione", che segnò l'inizio della sua notorietà.
Collaborò con diverse Università, ad esempio il MIT, l'Istituto di scienze applicate di Princeton, il CNRS di Parigi dopo aver ottenuto una borsa di studio della Fondazione Rockefeller.
- Nel 1962 iniziò la sua ricerca in matematica applicata su oggetti definiti con modelli classici, in particolare la curva di Koch e il famoso fiocco di neve di Koch.
- Nel 1967 integrò nei suoi studi ricerche più complesse, concentrandosi su oggetti con dimensione non intera, ispirandosi al concetto di dimensione di Hausdorff.
Così, come ti sarà spiegato nelle ore di ripetizioni matematica, a differenza dei modelli classici, Mandelbrot si interessò alle strutture complesse e disordinate presenti in natura, il che lo portò alla scoperta dei frattali.
La sua opera principale in cui introdusse la nozione di frattale, è "Oggetti frattali: forma, caso e dimensione" (1975). Qui esplorò il modo in cui queste forme complesse e irregolari, presenti in natura, obbediscono a specifiche regole matematiche.
Quanto è lunga la costa britannica
Apertura del documento di ricerca di Benoît Mandelbrot sui frattali, 1973
Ecco il problema posto fin dall’inizio: a causa della sua irregolarità, la costa bretone è difficile da misurare con precisione. Se è possibile calcolarne una distanza globale, è invece complicato tener conto di ogni singola curva della costa. Questo è il tema del primo articolo scientifico di Mandelbrot sull’argomento.
Ciò portò alle prime riflessioni sul fatto che semplici leggi matematiche governano in realtà paesaggi naturali come le montagne: questo è l'inizio della teoria dei frattali!
Negli anni ’70, Mandelbrot formalizzò e rese popolare il concetto di frattali, in particolare con l’insieme di Mandelbrot, che diventò un’icona della matematica visiva.
Capire l'insieme di Mandelbrot
Per capire, bisogna prima osservare. Quindi inizia a guardare l'insieme di Mandelbrot e scopri le infinte forme che contiene effettuando degli zoom:
Nel 1973, Mandelbrot firmò un articolo scientifico destinato a cambiare la sua carriera e la percezione dei suoi colleghi riguardo ai numeri interi e alle forme definite – o meglio, indefinite: Forme nuove del caso nelle scienze. In questo contesto, presentò oggetti fino ad allora poco conosciuti, come il triangolo di Sierpinski e il fiocco di Koch.
I punti salienti di questo articolo:
- L’importanza delle fluttuazioni obbligatorie
- La non esistenza di un’unica forma di caso, che porterebbe sempre a un’equalizzazione secondo la legge dei grandi numeri
- I fenomeni naturali obbediscono invece a un altro tipo di casualità, in cui la legge dei grandi numeri non è applicabile
- Questi fenomeni seguono il concetto di "autosimilarità" (una proprietà dei frattali, in cui una struttura si ripete identica o simile a sé stessa su scale diverse).
durante la sua prima lezione ad Harvard

Diversi principi definiscono questo complesso insieme:
Connessione
L’insieme di Mandelbrot è considerato localmente connesso. Significa che in un’area limitata è possibile connettere qualsiasi punto senza dover attraversare punti fuori dall’insieme. In altre parole, non ci sono "buchi" o "divergenze" tra i punti vicini all’interno dell’insieme.
Autosimilarità
L’insieme di Mandelbrot è considerato autosimile nei punti vicini: se zoomiamo su una piccola parte dell'insieme, possiamo vedere strutture simili a quelle dell'insieme globale, ma non in modo perfetto. Non è una simmetria perfetta, ma una ripetizione di schemi che si assomigliano, anche se a scala diversa.
Universalità
Il suo comportamento complesso appare in una vasta gamma di sistemi dinamici e funzioni matematiche. La sua struttura è rappresentativa di un'intera classe di frattali e non dipende da un caso specifico, ma è applicabile a diversi modelli matematici.
Questo si ispira ad altri insiemi, come l'insieme di Julia, teorizzato da Gaston Julia e Pierre Fatou all'inizio del XX secolo. L'insieme di Mandelbrot e gli insiemi di Julia sono strettamente legati dall'iterazione della funzione complessa zₙ₊₁ = zₙ² + c.
L'insieme di Mandelbrot serve da "mappa" degli insiemi di Julia:
- Ogni punto c di Mandelbrot corrisponde a un insieme di Julia specifico.
- Se c appartiene a Mandelbrot, l'insieme di Julia associato è connesso; altrimenti, è totalmente discontinuo.
Questa relazione rivela una struttura profonda tra stabilità e caos, in cui Mandelbrot raccoglie l'infinità delle forme frattali di Julia. Insieme, offrono una comprensione visiva e dinamica dei sistemi complessi in matematica e fisica.
Applicazioni dei frattali di Mandelbrot
L'insieme di Mandelbrot deve la sua popolarità alla ricchezza delle sue forme, alla complessità infinita dei suoi dettagli e alla possibilità di esplorarlo grazie ai numerosi software disponibili.
È basato su una semplice equazione iterativa, che produce forme complesse e infinite, rendendolo un oggetto matematico unico. Chiedi al tuo insegnante di ripetizioni matematica torino di parlartene. Infatti:
- Il fattore di ingrandimento raggiunge circa 60 miliardi: su scala reale, la prima immagine dello zoom sarebbe dieci volte più grande della distanza Terra-Luna.
- Questa esplorazione può essere prolungata fino a un fattore di ingrandimento di 10³⁰.
- Ogni zoom rivela dettagli sempre più sottili, illustrando la natura ricorsiva dei frattali.
L'insieme di Mandelbrot affascina per i suoi motivi estetici, che mescolano rigore scientifico e bellezza visiva, creando un legame tra matematica e arte. L'insieme è stato infatti fonte di ispirazione per il design grafico, la musica e l'animazione, in cui i motivi frattali arricchiscono le opere digitali.
Oltre a questo, i frattali di Mandelbrot offrono due principali opportunità nel campo della scienza e della matematica:
L'ottimizzazione tecnologica delle immagini e delle telecomunicazioni:
- nell'elaborazione delle immagini, i frattali consentono di comprimere i file in modo efficiente, preservandone i dettagli essenziali.
- Nelle telecomunicazioni, le antenne frattali migliorano la ricezione e riducono l'ingombro garantendo prestazioni multibanda.
La modellizzazione dei fenomeni naturali, formati biologicamente da frattali:
siccome si trovano in natura (nella vegetazione) o in geologia (montagne formate dall'erosione), i frattali consentono di modellizzare con precisione numerosi fenomeni naturali, riproducendone le forme complesse e auto-simili, ad esempio per quanto riguarda le formazioni nuvolose o temporalesche.
L'insieme di Mandelbrot ha dato origine a una nuova classe matematica, poiché non rientra nei canoni tradizionali della geometria euclidea o dell'analisi classica. È infatti organizzato secondo i principi di autosimilarità e complessità infinita. Altri ricercatori si sono ispirati a questi studi per sviluppare le proprie ricerche a partire dagli anni ’70.
In questa tabella possiamo vedere esempi di applicazioni dei frattali in diversi ambiti!
| Settore | Applicazione dei Frattali |
|---|---|
| Matematica | Modello per studiare e comprendere forme irregolari e caos |
| Fisica | Simulazione di fenomeni complessi come la turbolenza nei fluidi |
| Biologia | Modelli di crescita naturale, come la ramificazione dei vasi sanguigni |
| Informatica | Compressione di immagini |
| Astronomia | Studio delle strutture cosmiche, come la distribuzione delle galassie |
| Arte e Design | Creazione di motivi complessi per opere artistiche e design grafico |
| Economia e Finanza | Modello per la previsione dei mercati finanziari (mercati frattali) |
L'eredità di Mandelbrot: un nuovo sguardo sulla natura

Benoît Mandelbrot ha dimostrato che i frattali permettono di modellizzare strutture cosmiche, come la distribuzione delle galassie.
L’universo presenta motivi auto-simili a diverse scale, dalla rete cosmica fino alle nebulose.
Il suo lavoro ha contribuito a
comprendere l'organizzazione caotica ma strutturata dell'universo, svelando un legame tra matematica e dinamiche cosmiche.
La scoperta di Mandelbrot ha trasformato la visione dei sistemi caotici e complessi, aprendo un nuovo campo e nuove prospettive scientifiche. In questo senso, i frattali offrono una comprensione più approfondita delle strutture naturali e delle dinamiche non lineari, costituendo uno strumento per esplorare l’infinito attraverso la matematica.
Il lavoro di questo matematico è fonte di ispirazione e innovazione fin dagli anni ’70 e continua a influenzare la scienza, l’ingegneria e l’arte, aprendo nuove prospettive nella ricerca. Tra gli esempi più rilevanti troviamo:
- Benoît Mandelbrot, insieme a Richard Hudson, ha applicato i frattali alla finanza, dimostrando che i mercati seguono modelli imprevedibili, lontani dalle curve gaussiane classiche.
- Michael Barnsley, matematico, ha sviluppato la compressione frattale delle immagini, una tecnica rivoluzionaria per l’archiviazione delle immagini sfruttando l’autosimilarità.
- Geoffrey West, fisico, ha utilizzato i frattali per spiegare le leggi di scala in biologia, in particolare il modo in cui i sistemi vascolari ottimizzano la distribuzione dei nutrienti.
Per approfondire il primo punto, puoi seguire una ripetizione matematica milano o ascoltare questo podcast:
L’insieme di Mandelbrot incarna la bellezza della matematica e il suo legame con il mondo naturale e quello della tecnologia. Ma esiste davvero un limite al lavoro di Mandelbrot? Sembrerebbe che abbia aperto la porta dell’infinito… La vera domanda è: fino a quando continueremo a scoprire cose nuove?
Riassumi con IA