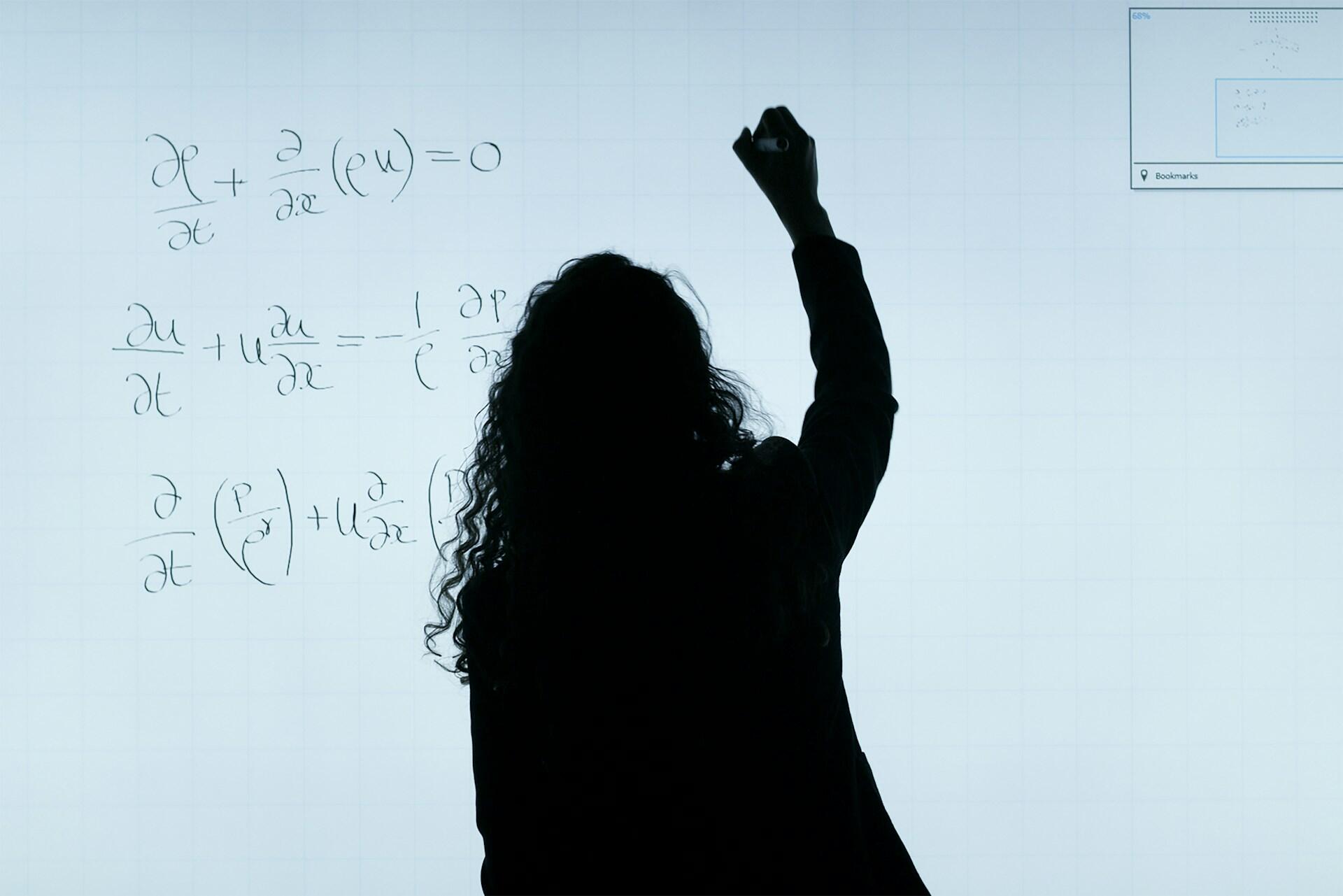Chi non conosce la matematica difficilmente riesce a cogliere la bellezza, la più intima bellezza, della natura.
R.P. Feynman
I frattali sono affascinanti strutture matematiche, caratterizzate da autosimilarità e complessità infinita a tutte le scale.
I frattali sono forme geometriche complesse che mostrano una proprietà speciale chiamata auto-similarità: ogni loro parte assomiglia al tutto, anche se ingrandita o rimpicciolita.
Teorizzati da Gaston Julia e poi divulgati da Benoît Mandelbrot, essi compaiono tanto in natura e in geologia quanto nella tecnologia, quanto in centinaia di ore di lezioni di matematica. Forme come il fiocco di neve di Koch o il triangolo di Sierpinski svelano un mondo in cui matematica ed estetica si fondono armoniosamente.
Per iniziare, ecco una tabella che riassume le principali caratteristiche:
| Caratteristica | Insieme di Julia | Insieme di Mandelbrot | Fiocco di neve di Koch | Triangolo di Sierpinski |
|---|---|---|---|---|
| Autore | Gaston Julia (1918) | Benoît Mandelbrot (1979) | Helge von Koch (1904) | Wacław Sierpiński (1915) |
| Tipo di struttura | Frattale complesso (nel piano dei numeri complessi) | Insieme parametrico (piano complesso) | Frattale geometrico lineare | Frattale geometrico bidimensionale |
| Forma iniziale | Punto complesso z₀ | Parametri c complessi | Triangolo equilatero | Triangolo equilatero |
| Autosimilarità | Sì (ma con variazioni complesse) | Sì (nelle ramificazioni del bordo) | Sì | Sì |
| Area | Dipende dal parametro c | Variabile, con bordi complessi | Finita | Tende a zero |
| Aspetto visivo | Da forme filiformi a “polveri” disconnesse | Figura cardioide con ramificazioni simmetriche | Bordo frastagliato simile a un fiocco di neve | Triangoli vuoti ricorsivi che formano una rete intricata |
| Applicazioni | Arte generativa, caos, dinamiche complesse | Estetica visiva, computer grafica | Fisica, modellazione delle superfici, grafica digitale | Reti, telecomunicazioni, geometria |

Decodificare l'insieme di Julia: un'immersione nell'infinito dei frattali
Per iniziare il lavoro di comprensione dei frattali, è impossibile non menzionare l'insieme di Julia, che è stato una figura fondante di questa teorizzazione.
Gaston Julia, nato in Algeria nel 1893, ebbe una prestigiosa carriera accademica come professore di matematica. Dopo aver conseguito il dottorato, insegnò all'École Normale Supérieure, dove formò diverse generazioni di matematici.
Prima del suo lavoro, i fondamenti teorici degli insiemi frattali e dei sistemi dinamici stavano già emergendo nel XIX secolo. Matematici come Pierre Fatou, Henri Poincaré e Félix Klein avevano esplorato i comportamenti complessi delle funzioni olomorfe e delle trasformazioni iterative.
cioè un valore incommensurabile, quasi infinito.
Ci sono 4 principi fondamentali che riguardano l'insieme di Julia, di cui puoi parlare con il tuo prof di ripetizioni matematica:
- Forma matematica: l'equazione di Julia si basa sull'iterazione della funzione quadratica complessa, dove i suoi fattori sono numeri complessi.
- Divergenza o stabilità: applicando ripetutamente questa funzione a un punto z, osserviamo se tende all'infinito (divergenza) o rimane in una zona limitata (stabilità).
- Definizione dell'insieme: l'insieme di Julia è formato dai punti z, le cui iterazioni non divergono. La sua forma dipende dal parametro c.
- Collegamento con Mandelbrot: l'insieme di Mandelbrot ordina i valori di c in base alla stabilità dell'insieme di Julia, collegando così le due strutture frattali.

L'insieme segue la seguente equazione:
 f_c(z) = z^2 + c
f_c(z) = z^2 + c
Le equazioni rientrano in due grandi categorie:
Gli insiemi connessi
un insieme in cui tutti i punti sono uniti in un’unica figura continua.
Gli insiemi totalmente disconnessi
o “polvere”, sono composti da punti o parti isolate che non sono collegate tra loro.
Così, al corso di matematica scoprirai che:
- Se un numero complesso c appartiene all'insieme di Mandelbrot, allora l'insieme di Julia corrispondente è connesso, ovvero forma una struttura continua.
Questi insiemi presentano forme filamentose e ricche di dettagli, che ricordano figure organiche come coralli, foglie o ramificazioni naturali.
Ad esempio, per c = 0, l'insieme di Julia è un disco semplice e perfettamente regolare.
Per altri valori complessi di c, la forma può diventare molto più intricata e affascinante. - Al contrario, se c non appartiene all'insieme di Mandelbrot, allora l'insieme di Julia associato è totalmente disconnesso: è composto da una miriade di punti separati, formando quella che viene detta "polvere di Fatou". Questi insiemi appaiono come strutture sparse e caotiche, in cui ogni punto è isolato dagli altri, senza alcuna connessione.
Software come Houdini o Mandelbulb3D permettono di generare ambienti ultra-dettagliati a partire da equazioni frattali, offrendo un’estetica al tempo stesso realistica e surreale.
Frattali cosa sono: ce lo spiega Mandelbrot
Un frattale è un oggetto geometrico fatto di parti in un certo senso simili al tutto
Benoit Mandelbrot
Fu Mandelbrot a introdurre la nozione di frattale, quella sopra è solo una delle tante definizioni che ha dato. Il merito di questo matematico è aver esplorato il modo in cui queste forme complesse e irregolari, presenti in natura, obbediscono a specifiche regole matematiche.

Collegando la geometria, il caos e le strutture naturali, ha dimostrato che i frattali offrono un nuovo linguaggio per comprendere il mondo, influenzando molti campi scientifici e artistici.
Nel 1973, Mandelbrot pubblicò un articolo scientifico che avrebbe cambiato la sua carriera e la percezione dei suoi colleghi delle questioni relative ai numeri interi e alle forme definite, o meglio, indefinite, che si concentrava su:
- L'importanza delle fluttuazioni obbligatorie
- La non-esistenza di una sola forma di caso, che porterebbe sempre a un'uguaglianza secondo la legge dei grandi numeri
- I fenomeni naturali obbediscono a un altro tipo di caso in cui non è possibile applicare la legge dei grandi numeri
- Questi fenomeni rispondono piuttosto a una omeotetia di scala, che sarà poi chiamata "autosimilarità".
I principi che definiscono l'insieme di Mandelbrot sono:
- Connettività
- Autosimilarità
- Universalità
L'insieme di Mandelbrot affascina per i suoi motivi estetici, che fondono rigore scientifico e bellezza visiva, creando un legame tra matematica e arte. Il tutto è stato fonte di ispirazione anche per la grafica, la musica e l'animazione, dove i pattern frattali arricchiscono le opere digitali grazie alla realtà aumentata.
Nel 1993, Mandelbrot ricevette il Premio Wolf per la fisica, "per aver trasformato la nostra visione della natura". Morì il 14 ottobre 2010, lasciando un'eredità che ha rivoluzionato la comprensione delle forme naturali e dei sistemi complessi.
I lavori di Mandelbrot sono una fonte di ispirazione e innovazione sin dagli anni '70 e continuano a influenzare la scienza, l'ingegneria e l'arte, aprendo nuove prospettive nella ricerca. Tra gli esempi più significativi, che puoi seguire durante i corsi matematica online, troviamo:
- Benoît Mandelbrot, in collaborazione con Richard Hudson, ha applicato i frattali alla finanza, dimostrando che i mercati seguono modelli imprevedibili, lontani dalle curve gaussiane classiche.
- Michael Barnsley, matematico, ha sviluppato la compressione frattale delle immagini, una tecnica rivoluzionaria per memorizzare immagini sfruttando l'auto-similarità.
- Geoffrey West, fisico, ha utilizzato i frattali per spiegare le leggi di scala in biologia, in particolare come i reti vascolari ottimizzano la distribuzione dei nutrienti.
Grazie a questa teoria, i frattali sono studiati da vari punti di vista, inclusi nella natura, con applicazioni alla vegetazione e alla geologia.

I frattali in natura: dalla vegetazione alle formazioni geologiche, tra caos e ordine

I frattali sono strutture ripetute presenti nella vegetazione.
Dagli alberi alle foglie, dai fiori alle radici, queste forme consentono una crescita ottimizzata.
Promuovono un migliore assorbimento della luce, una circolazione efficiente dei nutrienti e l'adattamento alle diverse situazioni ambientali.
Per comprendere i frattali naturali, è importante capire che essi possono essere riscontrati a diverse scale nella nostra vita quotidiana, sia su scala microscopica (ad esempio nei fiocchi di neve) che su larga scala (nelle nuvole o montagne).
Così, si parla di frattali vegetali e geologici per indicare una realtà che è stata concettualizzata e espressa da Mandelbrot.
Le nuvole non sono sfere, le montagne non sono coni, le coste non sono archi di cerchio, la corteccia di un albero non è liscia e il fulmine non segue una linea retta. La natura è complessa e la geometria frattale rende conto di questa complessità e permette di studiarla.
Benoit Mandelbrot
Frattali vegetali
In natura la crescita delle piante segue spesso schemi frattali. Queste strutture consentono alle piante di ottimizzare il loro sviluppo massimizzando l'esposizione alla luce, l'efficienza del trasporto dei nutrienti e l'adattamento alle condizioni ambientali.
Si distinguono quindi tre grandi insiemi per proprietà specifiche:
- 🌳 Gli alberi e i loro rami
- 🌸 I fiori e i loro semi
- 🍃 Le foglie e le loro vene
Le foglie presentano modelli frattali nei loro sistemi nervati, che assicurano un'efficiente distribuzione di acqua e minerali. Questa rete ottimizza inoltre la resistenza della foglia e consente una riparazione più rapida in caso di danni.
Frattali geologici
I frattali sono presenti anche in molti fenomeni geologici, rivelando l'equilibrio tra ordine e caos in natura. Questi schemi ripetitivi ci consentono di comprendere meglio l'evoluzione del paesaggio terrestre e di migliorare i modelli scientifici legati alle dinamiche geologiche e ambientali.
Le linee costiere irregolari, con insenature, baie e promontori, sono esempi di frattali geologici. La loro complessità rimane simile indipendentemente dalla scala di osservazione, a causa dei processi di erosione e sedimentazione che le modellano nel tempo.
Le forme frattali osservate in natura non sono frutto del caso, ma il risultato di processi geologici che trasformano gradualmente il paesaggio:
- L'erosione, causata dall'acqua, dal vento o dal ghiaccio, scolpisce montagne, valli e coste in strutture irregolari che si ripetono a diverse scale
- La sedimentazione, che accumula gradualmente particelle trasportate dall'acqua o dal vento, modella i delta dei fiumi e le dune con forme frattali, con modelli che si ripetono nei depositi successivi
- Le reazioni chimiche contribuiscono alla formazione di cristalli e minerali con strutture frattali, come i dendriti di manganese che ricordano i rami degli alberi
I frattali svolgono un ruolo fondamentale nella comprensione e nella simulazione di fenomeni naturali complessi , tra cui la meteorologia e altre discipline.
Un esempio concreto di questo frattale naturale non è altro che il fiocco di neve di Koch, l'incarnazione della geometria frattale.
Il fiocco di neve di Koch, una perfetta introduzione ai frattali

Il fiocco di neve di Koch è una figura iconica della geometria frattale, che illustra l'idea di una struttura infinitamente complessa a partire da un processo semplice.
Progettato da Helge von Koch all'inizio del XX secolo, si basa su una costruzione iterativa che genera una forma autosimile.
Il fiocco di Koch è costruito a partire da un semplice triangolo equilatero, su cui un processo di iterazione aggiunge progressivamente complessità. Questo principio, simile a quello utilizzato per generare il triangolo di Sierpinski, si basa su una modifica sistematica dei segmenti della figura:
- A ogni passaggio, ogni segmento della struttura viene diviso in tre parti uguali
- Una punta triangolare viene aggiunta al centro
- In questo modo si crea una successione infinita di nuovi vertici
- Più si applicano iterazioni, più la figura diventa complessa, generando una forma che sembra mantenere sempre lo stesso aspetto generale, qualunque sia il livello di ingrandimento
Per disegnare il fiocco di Koch si può usare uno strumento come un software di disegno vettoriale o un linguaggio di programmazione, strumenti come Python con Turtle, GeoGebra o Inkscape permettono di automatizzare questa costruzione regolando il numero di iterazioni per osservare la crescente complessità del frattale.
Se il fiocco di Koch trova applicazioni in ambiti come la grafica e l'informatica, è anche noto per il suo legame con altri frattali presenti in natura, in particolare in fisica e in biologia. Viene infatti utilizzato per studiare la crescita frattale di materiali e organismi.
- Nel campo della fisica, il fiocco di Koch svolge un ruolo chiave nello studio della crescita frattale dei materiali. Viene impiegato nell'analisi delle superfici rugose, dove permette di studiare la diffusione della luce o la conducibilità termica.
- Nella fisica del plasma, aiuta a modellizzare alcune forme complesse di propagazione.
- In biologia, schemi simili si ritrovano nella formazione di alcuni tessuti e organismi, come le strutture ossee o le reti vascolari.
Un altro frattale con proprietà simili è il triangolo di Sierpinski!
Forme complesse in geometria: il triangolo di Sierpinski

Il triangolo di Sierpinski è un frattale scoperto nel 1915 dal matematico polacco Wacław Sierpiński.
La sua costruzione si basa su un semplice processo iterativo, che può essere eseguito manualmente o utilizzando un programma per computer.
Dal punto di vista matematico, il triangolo di Sierpinski illustra proprietà fondamentali delle frattali, in linea con altre teorie come l’insieme di Julia, pioniere in questo campo. È autosimile, il che significa che qualsiasi parte della figura è una replica ridotta dell’insieme.
La sua dimensione frattale non è un intero, a differenza degli oggetti geometrici classici, e viene calcolata tramite la seguente relazione:
 d = \frac{\log 3}{\log 2} \approx 1.585
d = \frac{\log 3}{\log 2} \approx 1.585
Il triangolo di Sierpinski ha area tendente a zero ma perimetro infinito!
Man mano che si applicano infinite iterazioni nella costruzione del triangolo di Sierpinski, si continuano infatti a rimuovere piccoli triangoli centrali. Anche se la figura sembra sempre più complessa, l'area totale tende a zero, perché a ogni iterazione si rimuove il 25% dell'area restante.
Tuttavia, il perimetro cresce all'infinito! E la struttura continua a esistere nello spazio come figura ben definita. Questo paradosso tra "area nulla" e "forma visibile infinita" è una delle stranezze che rendono le frattali così affascinanti — e così diverse dalla geometria classica.
Per maggiori dettagli, puoi consultare il nostro articolo approfondito sul triangolo di Sierpinski. Questo popolare triangolo ha ispirato numerose applicazioni, sia nelle telecomunicazioni, nelle reti o nella natura, ma anche nel mondo dell'animazione e dei videogiochi.
Riassumi con IA