La matematica pura è, a suo modo, la poesia delle idee logiche.
Albert Einstein
Saper disegnare il grafico di una funzione è molto importante, soprattutto perchè potrebbe far parte delle domande di matematica all'esame di maturità!
Solitamente i problemi possono riguardare le funzioni polinomiali, esponenziali, logaritmiche e trigonometriche, ma per risolverli non devi avere dubbi su come disegnare il grafico di una funzione.
Le funzioni sono strumenti fondamentali in matematica, utilizzati per modellare fenomeni, descrivere relazioni tra grandezze e costruire concetti astratti in molti rami della disciplina.
Il grafico di una funzione è la rappresentazione visiva di una funzione in un sistema di coordinate. Esso consente di comprendere il comportamento della funzione associando i punti del dominio (asse x) ai corrispondenti valori del codominio (asse y) in uno spazio bidimensionale.
Ina rappresentazione grafica è l'ultimo tassello nello studio delle funzioni: lo studio di funzione consiste nell’analizzare tutti i valori che si possono assegnare alle variabili, identificarne i limiti, i punti di flessione, trovare gli asintoti, se esistono, e infine rappresentare la funzione con un grafico.
Esiste un metodo matematico generale per studiare le variazioni di una data funzione in un intervallo I, tracciare le variazioni e rappresentare il grafico su un piano cartesiano.
Scopriamo dunque tutto ciò che bisogna sapere per tracciare correttamente il grafico di una funzione!

Definizione e grafico di una funzione lineare
Lo studio della funzione lineare è senza dubbio il più semplice in assoluto.
Ricordiamo innanzitutto che una funzione è un'associazione che collega gli elementi di due insiemi: a ogni elemento dell'insieme A corrisponde uno e un solo elemento di B.
In altri termini, a ogni valore della variabile x corrisponde un solo valore della variabile y.
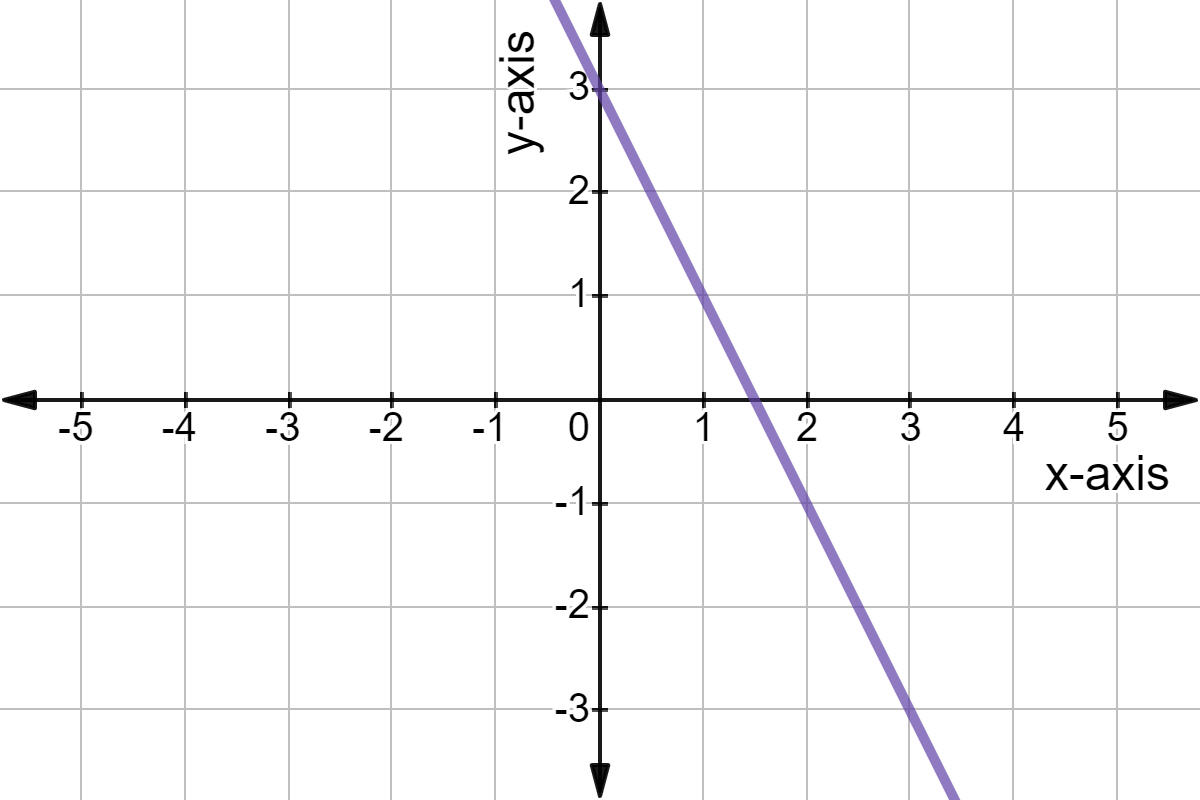
Se la funzione parte da A, questa è la variabile indipendente e l'insieme è definito dominio, mentre B, la variabile dipendente, diventa il codominio. Possiamo dire che B, o variabile y, varia al variare di A, o variabile x.
Le funzioni lineari sono rappresentate tramite una retta sul piano cartesiano, ossia il piano formato da due rette perpendicolari, una retta orizzontale o asse delle x o delle ascisse, e una retta verticale o asse delle y o delle ordinate.
La caratteristica delle funzioni lineari è che nell'equazione presentano una sola variabile e una sola costante, detta anche parametro, diversa da zero:
f (x)= ax +b
Si tratta, quindi, di un polinomio di primo grado dove:
- a è diverso da zero
- b un numero reale qualunque
Il parametro è detto anche coefficiente angolare perché determina l'inclinazione della retta. Se il parametro è a= 0 abbiamo una funzione costante. Nel caso in cui b sia uguale a zero abbiamo una funzione identità.
Andando al grafico, come abbiamo visto, si tratta di una retta il cui punto di intersezione tra i due assi corrisponde a x=0. La retta non sarà né verticale né orizzontale ma avrà una pendenza descritta dal valore di a. Se per esempio nella funzione y=ax+b il valore di a è 3, vuol dire che per ogni punto sulle ascisse, ci sposteremo di 3 punti sulle ordinate.
Grazie alla pendenza si possono individuare altri punti e usare degli strumenti molto semplici, come il righello e la squadra per disegnare il grafico della funzione lineare. Basterà trovare tre punti per poter tracciare la retta.

Nel caso delle funzioni complesse, che non sono lineari, è comunque utile partire sempre dai punti di intersezione con l'asse delle ascisse dove x è pari a zero.
Cerchi lezioni di matematica a Roma?
Disegnare il grafico di una funzione derivata prima
In analisi matematica, il concetto di derivata è fondamentale, soprattutto per gli studenti di quinta superiore.
La derivata misura il tasso di variazione di una funzione f(x) al cambiamento del suo argomento (x). In parole semplici, indica quanto incrementa o decresce la funzione punto per punto.
Il rapporto tra la distanza sull'asse delle y e quella sull'asse delle x si chiama rapporto incrementale. La derivata fotografa la situazione di un punto specifico di questo rapporto se esiste un limite ed è finito.
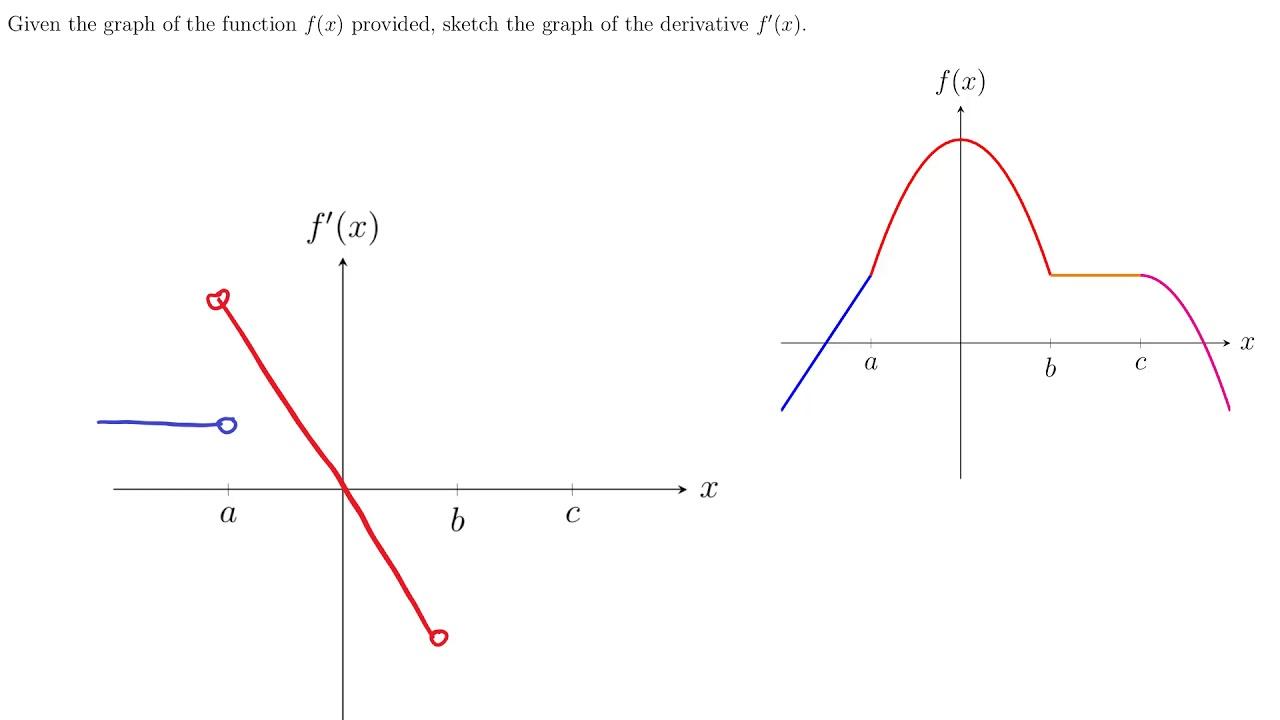
Ci dice se la funzione accelera o decelera in quel punto preciso, per questo trova applicazione in fisica, economia, statistica.L'insieme dei punti in cui si può calcolare la derivata prima (f') è una funzione derivabile.
La derivata seconda (f'') è l'insieme dei punti in cui si può calcolare la derivata prima, quindi è la derivata della derivata prima. Dal punto di vista geometrico, la derivata seconda serve a identificare i valori che rendono una curva concava, mentre la derivata prima ne rappresenta l'inclinazione.
Prima di disegnare una funzione, assicurati di avere gli strumenti necessari o un foglio Excel, per raccogliere i valori dell'insieme dominio e creare grafici.
In questa nostra ripetizione matematica online prendiamo in esame la funzione f(x)=x³+3²-9x+6. Si tratta di una funzione polinomiale formata dalla somma di 3 termini della formula axn (a e n sono numeri interi naturali) e una costante. Sapendo che la derivata di axn è del tipo anxn-1 e che la derivata di una costante è zero, la derivata di f(x) è:
f'(x)=3x²+6x-9.

Fattorizzare la derivata di f
Lo scopo di questa fase è fattorizzare la derivata della funzione f(x) per poterla esprimere sotto forma di prodotto o quoziente di un’espressione.

La fattorizzazione è una tappa chiave da non dimenticare perché rende molto più facile lo studio del segno della funzione f'(x). La fattorizzazione, è come risolvere un enigma matematico durante una lezione di tale materia!
Piccola curiosità: lo sapevi che il calcolo della derivata di una funzione in fisica serve a misurare l'accelerazione dei corpi?
Possiamo prendere 3 come fattore e scrivere: f'(x)=3(x²+2x-3).
x²+2x-3 è un trinomio di secondo grado che ha la forma ax²+bx+c dove a,b, e c sono numeri reali. Per fattorizzare questo trinomio bisogna innanzitutto calcolare il discriminante e trovare le radici di x1 e x2:
b2 -4ac = 22 -4×1×-3 = 4+12 = 16
Si può allora calcolare la radice con la seguente formula:
x1=-3
x2=1
Si noti che il discriminante è positivo (e allora le due radici esistono), il trinomio può essere scritto sotto la forma fattorizzata (x-x1)(x-x2), che vuol dire x²+2x-3=(x-(-3)) (x-1)=(x+3)(x-1).
La derivata della funzione si scrive nella seguente forma fattorizzata:
f'(x)03(x+3)(x-1)
Studiare il segno su un intervallo I
Il numero 3 è positivo quindi il segno di f’(x) è identico al segno di (x+3)(x-1).
Risolviamo la seguente disequazione:
x + 3 > 0 => x > -3, quindi il binomio x+3 è positivo se x è superiore a -3, è nullo se x è uguale a -3, ed è negativo se x inferiore a -3.
x – 1 > 0 => x > 1, allo stesso modo il binomio x-1 è positivo se x è superiore a -1, è pari a zero se x è uguale a 1 ed è negativo se x è inferiore a 1.
Il grafico del segno della derivata f'(x) è rappresentato qui sotto:
| GRAFICO DERIVATA | |||
|---|---|---|---|
| x | – ∞ | -3 1 | +∞ |
| x + 3 | – 0 + + | ||
| x – 1 | – – 0 + | ||
| f'(x) | + 0 – 0 + |
Si noti che avremmo potuto determinare il segno del trinomio x²+2x-3 usando anche un altro metodo. Quando il discriminante è positivo, il trinomio ax²+bx+c assume un segno contrario ad a nell’intervallo compresso tra le due radici x1 e x2 e lo stesso segno di a in caso contrario.
E dopo questa spiegazione, scopri come risolvere gli altri problemi matematici!
Tracciare la curva delle variazioni di f su un intervallo
Si trovi la derivata di f per ogni intervallo J:
- se f'(x)>0 per ogni x che appartiene a J, f è crescente
- se f'(x)<0 per ogni valore di x appartenente a J, f è decrescente.

L’andamento della curva è la rappresentazione schematica delle direzioni che prende la curva sull’asse delle ascisse e delle ordinate.
L’andamento della variazione di f è come segue:
| CURVA DELLE VARIAZIONI DI F | |||
|---|---|---|---|
| x | -∞ | -3 1 | +∞ |
| f(x) | 33 +∞-∞ 1 |
Si noti che f(-3)=33 e f(1)=1
Calcoliamo i limiti della funzione:
= = +∞
= = -∞ (un numero negativo soggetto a una potenza dispari, rimane negativo)
Dalla tabella delle variazioni di f, si nota che questa funzione raggiunge il massimo nel punto A (-3;33) e un minimo nel punto B (1;1).
Se ti interessa questo argomento, approfondisci anche la conoscenza delle equazioni in matematica!
Come rappresentare una funzione su un intervallo definito
Per tracciare il grafico che rappresenta questa funzione, basta posizionare il suo massimo e il suo minimo sul piano cartesiano e fare una tabella che ci aiuti a posizionare qualche altro punto preciso:
| x | f(x) |
|---|---|
| -5 | 1 |
| -2 | 28 |
| -1 | 17 |
| 0 | 6 |
| 5 | 161 |
Ed ecco la nostra famosa curva:
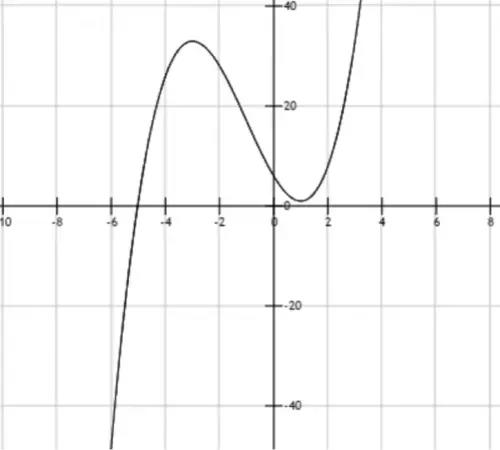
La matematica e l’arte spesso sono legate, solo che una curva matematica è tutto tranne che artistica! Fai attenzione a mettere i dati sul punto giusto del piano. La tabella delle variazioni di una funzione serve a trovare facilmente gli asintoti. In genere si trovano con lo studio del segno della derivata.
Durante un corso di matematica gli allievi si esercitano su tabelle che non rappresentano l’intera funzione, ma solo una una parte.
D’altronde, se una funzione si ripete all’infinito, non si può fare altrimenti. In questo caso, le funzioni sono dette periodiche.
Con queste semplici informazioni puoi ora disegnare con facilità il grafico di una funzione...buon lavoro!
Riassumi con IA