La matematica universale è la logica dell'immaginazione.
Gottfried Wilhem Leibniz
Durante le lezioni di matematica alle medie e alle superiori gli studenti iniziano a studiare le basi della statistica e della geometria, in particolare il calcolo della media e della mediana.
La grande incompresa tra queste variabili è la mediana, un indicatore centrale nell'analisi delle probabilità, delle dimostrazioni di geometria e dell'analisi statistica.
La mediana è un concetto statistico che rappresenta il valore centrale di un insieme di dati, quando questi sono ordinati in modo crescente o decrescente. La mediana divide il campione di dati in due metà: il 50% dei dati ha valori inferiori alla mediana e il restante 50% ha valori superiori.
Sapere calcolare la mediana è importante per diversi motivi, sia in statistica che nella vita di tutti i giorni, perché fornisce una misura affidabile della tendenza centrale di un set di dati. La mediana è semplice da interpretare, il che la rende utile in molte applicazioni pratiche in cui si cerca di comprendere la posizione di un valore all'interno di un gruppo di dati.
Superprof oggi veste i panni del tuo insegnante di ripetizioni matematica per aiutarti a capire la mediana cos'è e come si calcola!

Cos'è la mediana in matematica?
Quando si desidera approfondire le proprie conoscenze di base in matematica è importante partire da una base solida costruita su definizioni chiare ed efficaci.
Pertanto prima di lanciarsi in calcoli interminabili, è bene capire cos'è la mediana.

Che cos'è, dunque la mediana?
La mediana rappresenta il valore centrale di una sequenza di valori ordinati dal più piccolo al più grande. La mediana in una serie di dati si trova calcolando la media dei due valori centrali quando i dati sono disposti in ordine crescente.
Per calcolare la mediana bisogna dunque seguire questo metodo:
- Sistemare i dati in ordine crescente
- Se il numero totale di dati nella serie è dispari, la mediana è il valore esattamente al centro
- Se il numero di dati è pari, la mediana è la media dei due valori centrali
Per comprendere meglio come funziona il calcolo della mediana proviamo a fare un esempio.
Calcolo della mediana di una sequenza numerica dispari
Un insegnante di nuoto deve formare due gruppi di allievi di livelli diversi, e per questo chiede a 9 nuotatori di percorrere la vasca a nuoto libero per rilevare il tempo impiegato da ciascuno.

I risultati raccolti sono:
30,6 - 29,1 - 32,9 - 35,1 - 30,0 - 36,4 - 31,7 - 35,5 - 33,9
Mettendo questi valori in ordine crescente avremo quindi:
29,1 - 30,0 - 30,6 - 31,7 - 32,9 - 33,9 - 35,1 - 35,5 - 36,4.
Il tempo mediano (la mediana) è 32,9: questo valore permette di classificare le prestazioni dei nuotatori in due categorie che hanno lo stesso numero di dati: da un lato, ci sono i giocatori con i tempi più alti, dall'altro quelli con i tempi più bassi.
Proviamo allora ad aggiungere un dato che ci porti a calcolare la mediana di una sequenza numerica pari.
Calcolo della mediana di una sequenza numerica pari
A questo corso di nuoto si aggiunge un altro allievo, il quale percorre la vasca in 28,7 sec.
La sequenza numerica sarà ora la seguente:
28, 7 - 29,1 - 30,0 - 30,6 - 31,7 - 32,9 - 33,9 - 35,1 - 35,5 - 36,4.
Per fare il calcolo della mediana del gruppo di nuotatori, dobbiamo calcolare la media dei due valori centrali: (31,7 + 32,9) / 2 = 32,3
Media e mediana: qual è la differenza?
Uno degli errori più comuni quando si studia la mediana è confonderla con la media. Vediamo dunque in cosa consiste il calcolo della media aritmetica e in cosa differisce dal calciolo della mediana e i loro rispettivi utilizzi in matematica e statistica.
La media aritmetica si calcola sommando tutti i valori presenti in un gruppo di dati e dividendo il risultato per il numero totale dei valori.
Risulta dunque evidente che si tratti di un calcolo che porta a un'informazione piuttosto diversa da quella prodotta dal calcolo della mediana!
Proviamo a fare nuovamente un esempio.
Il reddito pro capite in Italia è di 31.641€. Dividendo questo valore per dodici mesi abbiamo uno stipendio mensile di 2.636 € a testa.
Questa cifra è la media, ma non ci dice nulla su come è distribuita la ricchezza.
Le persone più ricche fanno salire la media, perché guadagnano sei volte in più rispetto alle persone meno benestanti.

Secondo l'Istat, infatti, il 20,1% della popolazione italiana, ossia 12,06 milioni di abitanti, è a rischio povertà perché guadagnano meno di 858 € al mese.
Questo è il motivo per cui è fondamentale il calcolo della mediana e dei quartili (25% e 75%) per capire come si comportano i dati da noi presi in esame.
Cerchi di risolvere un problema con gli intervalli?

Come si calcola la mediana in una serie statistica discreta?
In statistica, una variabile è discreta quando contiene un numero definito di valori reali.

Scopriamo allora come si calcola la mediana in una serie statistica discreta:
1. Ordina i dati: assicurati che la serie statistica sia ordinata in senso crescente
2. Conta il numero totale di osservazioni: determina il numero totale di dati, che chiameremo n. Se i dati hanno frequenze associate (distribuzione di frequenza), conta il totale delle frequenze.
3. Determina la posizione della mediana:
- Se n è dispari la mediana equivale a (n+1)/2° valore.
- Se n è pari: La mediana è la media aritmetica dei valori nelle posizioni (n/2) e (n+1)/secondo valore.
4. Calcola la mediana: una volta trovata la posizione della mediana, individua il valore corrispondente.
Ma vediamo insieme un esempio: prendiamo il numero di messaggi inviato dai ragazzi del secondo liceo nella chat di classe. Supponiamo che la distribuzione dei messaggi inviati sia:
5, 12, 11, 10, 6, 17, 11, 12, 10, 13, 9, 11, 12, 8, 7, 10, 11, 10, 12, 11, 9, 10, 8, 11.
Disponiamo i valori in ordine crescente e inseriamo questa serie in una tabella, scrivendo i valori in ordine crescente e accanto, le persone a cui fanno riferimento.
Otteniamo dunque:
Xi: 5, 6, 7, 8, 9, 10, 11, 12, 13, 17 (serie di dati in ordine crescente)
N1: 1, 1, 1, 2, 2, 5, 6, 4, 1, 1 è il numero degli studenti che hanno inviato i messaggi
Se prendiamo i dati cumulati possiamo organizzarli in categorie: 12 studenti hanno inviato meno di 10 messaggi.
Calcolare la frequenza crescente cumulata ci permette di esprimere i valori dei risultati in percentuali.
Puoi ora calcolare la mediana per dati raggruppati; nel nostro caso Ni è un numero pari, 24. La mediana che separa il numero di individui della nostra serie in due parti uguali è la media di (N/2) e (N+1)/secondo valore. Dobbiamo quindi calcolare la media tra il 12° e il 13° dato.
La mediana Me è quindi pari a 10,5!
Se vuoi approfondire questo argomento trova lezioni di matematica nella tua zona: potrai anche scoprire come scrivere un algoritmo e calcolare il quoziente!
Calcolo della mediana di una serie continua
I dati di cui dobbiamo trovare la mediana possono essere numeri finiti o un numero incalcolabile di valori. Il primo passo consiste nel calcolare la curva delle frequenze cumulate crescenti per identificare la mediana e il quartile della serie.
Prendiamo un esempio semplice: vogliamo misurare la percentuale della popolazione che ha uno stipendio compreso tra 500 € e 2.100 € al mese.
Supponiamo che la distribuzione del reddito sia la seguente:
| Numero di persone | Stipendio mensile (€) |
|---|---|
| 40 | 500-800 |
| 31 | 800-1.100 |
| 25 | 1.100-1.200 |
| 52 | 1.200-1.500 |
| 37 | 1.500-1.800 |
| 18 | 1.800-2.000 |
| 27 | 2.000-2.100 |
Il totale dei dati N, è 230 persone. Calcoliamo poi la frequenza e la frequenza cumulata.
Puoi rappresentare la frequenza cumulata su un piano cartesiano, mettendo nelle ascisse i valori e nelle ordinate, le frequenze cumulate: possiamo in questo modo leggere la mediana anche graficamente, senza dover passare per il calcolo matematico:
Possiamo vedere chiaramente che la mediana della nostra scala è 13, a cui corrisponde un salario medio di 300 €.
Proviamo dunque a fare un'analisi di questo esempio:
- I quartili che si trovano al 25% e la 75% hanno rispettivamente dei valori di 9,7 e 17.
- Il 25% dei valori della serie è inferiore o pari a 9,7. Il 75% dei valori è inferiore o pari a 17.
- Il 25% dei valori sono compresi tra 17 e 21.
- Il 25% della popolazione attiva ha uno stipendio inferiore a 970 € al mese, mentre il 75% delle persone guadagna meno di 1.700 €.
- Il 25% del nostro campione guadagna tra 1.700 e 2.100 € al mese.
Potrai dunque divertirti a calcolare altri decili e centili per vedere qual è la dispersione del reddito di una classe di popolazione data!
Sapevi con la matematica puoi realizzare un cono perfetto ed eseguire la tassellatura di ogni superficie? Perchè non approfondire questi temi con delle lezioni di matematica a Roma!
Come si calcola la mediana in geometria?
Anche in geometria la mediana è molto utilizzata, soprattutto quando si rappresenta il triangolo.In tutti i programmi di matematica, a partire dalle medie, troviamo la nozione di mediana di un triangolo.
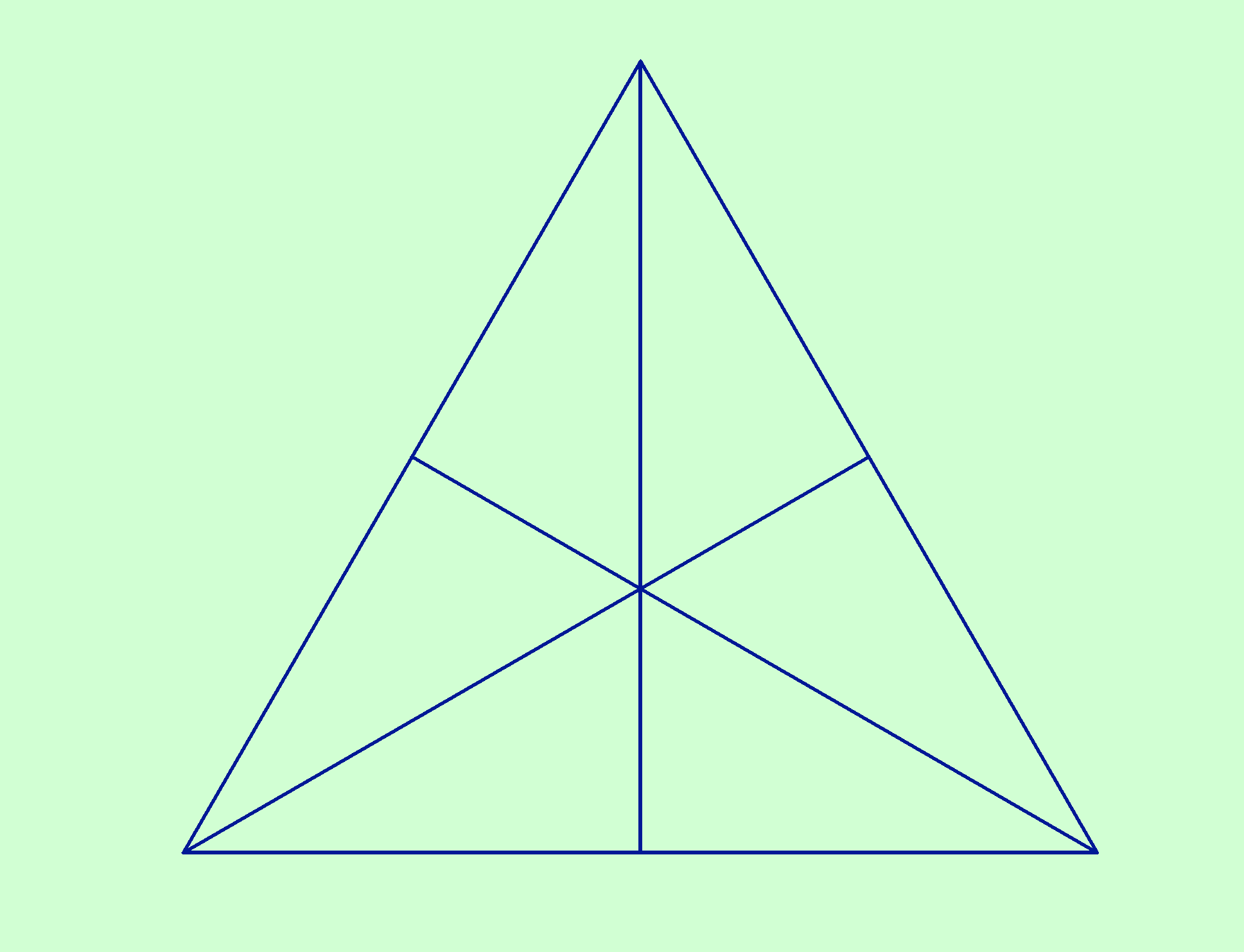
La mediana di un segmento è la retta che passa per il punto medio di questo segmento e il vertice opposto.
In un triangolo ABC, la mediana è il segmento che unisce i tre vertici con il punto medio del lato opposto, vale a dire il segmento AI, dove I è il punto medio del lato AB.
Supponiamo che i segmenti AI e IB abbiano la stessa lunghezza perché il nostro è un triangolo isoscele. L'area del triangolo AB è uguale a quella del triangolo ACI.
Questo ci permette di introdurre un tema centrale in geometria, il teorema della mediana:
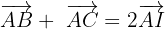
Le mediane dei tre lati del triangolo si intersecano al centro della figura in un punto che viene chiamato baricentro: il centro di gravità del triangolo.
Inoltre:
- In un triangolo isoscele, con due lati uguali, quindi, anche le due mediane avranno la stessa lunghezza.
- In un triangolo rettangolo, la mediana che parte dal vertice opposto all'angolo retto, misura la metà dell'ipotenusa.
Se hai difficoltà nel calcolo della mediana, a svolgere espressioni algebriche, a scrivere l'enunciato di una congettura matematica , a fattorizzare i polinomi perchè non prendere ripetizioni di matematica a Torino?
Sulla nostra piattaforma, Superprof, potrai trovare insegnanti di matematica esperti che sapranno esserti di aiuto nel colmare le tue lacune!
Résumer avec l'IA :
















E se ci sono sei numeri come si fa?
Ciao Alessandro,
se la serie di numeri è pari, dovrai prendere i due numeri centrali e farne una media per ottenere la mediana. Se ad esempio hai la serie di numeri 4,7,2,9,5,1 dovrai prima di tutto ordinarli dal più piccolo al più grande, quindi 1,2,4,5,7,9 e poi individuare i due elementi centrali (4 e 5) e farne una media: otterrai così la mediana, che in questo caso è 4,5.
si fa la media tra i due numeri centrali
è stato molto utile questo articolo! Grazie mille :)
Ci fa molto piacere che l’articolo sia stato di tuo gradimento!
Se lo stesso numero nella mediana si ripete più volte come si può fare?
Ciao Elena,
Quando calcoli la mediana di un insieme di dati e il numero mediano si ripete più volte, il processo per determinarla non cambia. La mediana è semplicemente il valore che si trova nel mezzo dell’insieme di dati quando questi sono ordinati in ordine crescente o decrescente. Se il numero di osservazioni è dispari, la mediana sarà il valore centrale. Se il numero di osservazioni è pari, la mediana sarà la media dei due valori centrali.
Grazie. Sono riuscito a risolvere il mio problema.
Ottimo, sono davvero felice che l’articolo ti sia stato d’aiuto! 😊 Se ti servisse una mano con altri concetti di statistica o matematica, sai dove trovarci. 📊✌️